Landau potential of ferroelectric liquid crystals
The Landau potential describes the order parameter through a phase transition. Using a method first derived by Giesselman et. al. [1,2] it is possible to determine the full Landau potential using the total polarisation and tilt angle of a ferroelectric liquid crystal system.
The difference in free energy density between the SmA* and SmC* phase, g-g0, in thin surface stabilised cells subjected to an electric field E is given by the generalised Landau free energy density as [3]:
| (1) |
where
• P is the total polarisation,
• Θ the tilt angle,
• α, b and c are the Landau expansion coefficients,
• C the bilinear coupling term,
• χ0 the dielectric susceptibility,
• Ω the biquadratic coupling coefficient and
• TC the related non chiral SmA to SmC transition temperature.
• TC is related to the respective chiral SmA* to SmC* transition TC* by:
| (2) |
Minimisation (1) with respect to P leads to the relation:
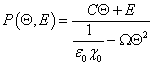 |
(3) |
A simultaneous fit of P(Θ,E) results in the determination of C, χ0 and Ω.
Minimisation of (1) with respect to the tilt angle and rearranging results in a non-trivial relationship between the tilt angle and temperature:
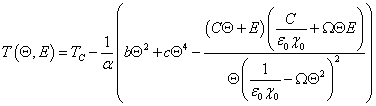 |
(4) |
A simultaneous fit of T(Θ,E) results in the determination of α, b, c and TC.
Substitution of (3) into (1) gives the difference in free energy density between the high temperature SmA* and the low temperature SmC* phase as:
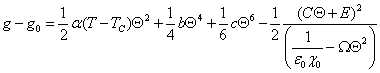 |
(5) |
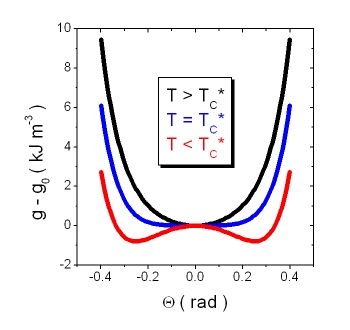
With all parameters known, (5) can be employed to visualise the full Landau potential on a quantitative basis for varying external conditions. As an example below, the temperature evolution of the Landau potential is shown above, at and below the SmA* to SmC* transition.